NOISE ANALYSIS - RESISTOR EXAMPLE
CIRCUIT
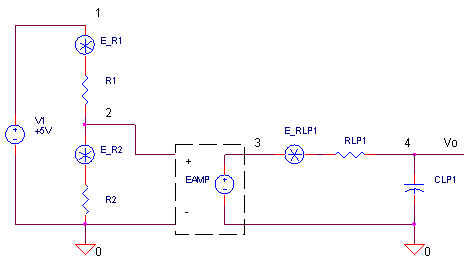
RES_NOISE.CR Download the SPICE file
You can't figure it out. You've taken one hundred samples of a 2.5V reference using a 16-bit ADC, but rarely are two consecutive readings the same. Okay, it's got to be noise, but where is it coming from? Unfortunately, one of our basic building blocks - the resistor - comes with its own inherent noise generator. But once we understand a little about the nature of this noise source, we have a few choices regarding how to reduce it.
RESISTOR NOISE
How is resistor noise modeled? Typically as a noise voltage in series with the resistor.
POWER SPECTRAL
DENSITY
The Power Spectral Density simply describes how much noise power
would generated by a resistor in a 1 Hz bandwidth.
S = 4 k T R (V2/Hz)
where
S = the noise Power Spectral Density
k = Boltzmans constant (1.38∙10-23)
T = temperature in Kelvin (Room temp = 27 °C = 300 K)
R = resistance
This noise power is the same at all frequencies - commonly called white noise!

NOTE! If you want to reduce the total noise in your circuit, then reduce your bandwidth!
VOLTAGE SPECTRAL
DENSITY
The Voltage Spectral Density is simply the square root of the power spectral
density.
N = ( 4 k T R )½ (V / Hz½)
Many manufacturers will specify the noise of their components (opamps for example) using these units. Notice the noise voltage units has the funky units of Volts per square root of the bandwidth. Later you'll see how to use N to calculate the RMS noise voltage in a circuit.
RESISTOR NOISE EXAMPLE
For a 100 kΩ resistor, let's find its power spectral density
S = 4 k T R
= 4 ∙1.38∙10-23 ∙ 300 ∙ 100k
= 1.66∙10-15 ( V2 / Hz )
and voltage spectral density
N = S ½
= (4 k T R) ½
= 40.7 ∙10-9 ( V / Hz½ )
(At first, 40 nV/Hz½ doesn't sound like much. But suppose your designing a low-noise design amplifier using a quiet op amp with an input voltage noise of only 4 nV/Hz½ . You wouldn't want to kill the party by using a 100k boom box as a feedback resistor. Smaller R values around 1k would be a better choice.)
CIRCUIT NOISE
How much noise will various resistors contribute at the output of your circuit? Four easy steps gets you the answer.
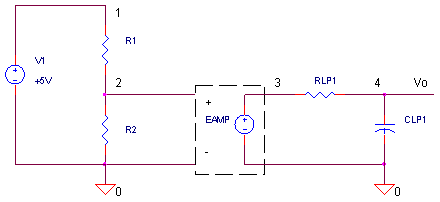
Let's walk through an example. Our circuit above is a simple resistor divider (Gain = 1/2) followed by an amplifier (Gain = 1) and a low-pass filter (fc = 1MHz). Let's assume we're seeking the noise density at low frequencies where the low-pass filter has no effect.
Step 1: Calculate S, the power spectral density from R1=100k.
S = 4 k T R
= 1.66∙10-15 ( V2 / Hz )
Step 2: Find A, the voltage gain A from the noise source to the output
A = R2/(R1+R2) = 1/2
then use A to calculate the output power spectral density from R1. (Notice A2 is actually used because we are dealing with power here.)
So = S ∙ A2
= 1.66∙10-15 ∙ (1/2)2
= 4.14 ∙10-16 (V2 / Hz)
Step 3. Repeat for all noise sources. For R2=100k, we get the same answer as R1
So = S ∙ A2
= 1.66∙10-15 ∙ (1/2)2
= 4.14 ∙10-16 (V2 / Hz)For RLP1=100, we get
So = S ∙ A2
= 1.66∙10-18 ∙ 1
= 1.66∙10-18 (V2 / Hz)
Step 4: Adding the contributions from all resistors we get a total power spectral density of
STOT = 4.14 ∙10-16 + 4.14 ∙10-16 + 1.66∙10-18
= 8.30 ∙10-16 (V2 / Hz)Now take the square root to get the total voltage spectral density of
NTOT = STOT ½
= ( 8.30 ∙10-16 ) ½
= 2.88 ∙10-8 ( V / Hz½ )
There you have it! At low frequencies, your resistors contribute a total
of 28.8 nV/ Hz½ at the
circuit's output.
WARNING!!! In this simple example, the gain (A) was found at low frequencies where the gain was flat. However, at higher frequencies, the low-pass filter rolls off the response. Real circuits include filters and amplifiers with gains that vary with frequency. Consequently, the noise calculations need to include these frequency effects! Sound fascinating? Yes! Sound like a pain in the can? Yes, again! Luckily, SPICE is equipped with the noise analysis tools.
SPICE NOISE ANALYSIS
The Noise Analysis essentially does the work in the above example for you. SPICE performs Noise Analysis together with an AC Analysis statement. For example, the statement
.NOISE V(4) V1 5
asks SPICE to calculate the equivalent noise at both output V(4) and V1 at every 5th frequency point in the AC analysis.
1. Calculate the power spectral density S from EACH resistor to output node V(4). This is performed at every 5th frequency point specified in the AC analysis.
2. Add noise contributions from all resistors to find the total power spectral density S and total voltage spectral density N at node 4.
3. Calculate the transfer function V(4) / V1 to determine the total voltage spectral density N referred to the input source V1.
CIRCUIT INSIGHT Simulate the SPICE file RES_NOISE.CIR. To recap, this circuit implements a simple resistor divider (Gain = 1/2) followed by an amplifier (Gain = 1) with a low-pass filter (fc = 1MHz).
Open the output file RES_NOISE.OUT to view the noise results. For every 5 th frequency of the AC analysis (100, 1000, 10000, ... Hz), SPICE prints out a nice noise summary. At 100 Hz for example, we see the power spectral density from each resistor R1, R2 and RLP1. Do the results match the densities calculated above? How about the total power and voltage spectral density, does it match our numbers above?
Seeing the noise from every resistor gives you some incredible insight! Why? It tells you who are the major contributors! Knowing the biggest noise makers, you can plan some noise reduction strategies - typically reducing bandwidth or resistor values.
HANDS-ON DESIGN Try lowering the resistors to values like R1 = R2 = 1 kΩ. What is the effect on total noise? Increase the gain of amplifier in the EAMP statement. How does it effect noise?
What have you noticed about the noise spectral density at high frequency? The noise begins to drop thanks to the low-pass filter RLP1 and CLP1. This could be a good thing! But of course, here's another one of life's balancing acts. Small bandwidth is good for low-noise, but not if it cuts into your signal's bandwidth!
Cool Feature SPICE let's you plot the total voltage spectral density N at the output V(4) or the input V1. Just add trace ONOISE or INOISE to the plot window. You can even add these variables to a .PRINT statement!
RMS VOLTAGE CALCULATION
Okay, enough noise versus frequency! What is the total RMS noise voltage in my circuit? You calculate this by multiplying the noise power density S by the bandwidth Δf, then taking the square root. For a flat bandwidth.
P = S ∙ Δf (V2)
E = ( P ) ½ (VRMS)
For a noise response that varies across the frequency spectrum, simply sum the noise power S at a number of frequency points fn = f1, f2, f3, ...
P = ∑ Sn ∙ Δfn (V2)
E = ( P ) ½ (VRMS)
where Sn is the power density at fn and Δfn = fn+1 - fn . How do you pick the number of frequency points. If the noise changes slowly versus frequency, you probably don't need many points. On the other hand, a rapidly changing noise vs. f requires more points effectively sample the spectrum.
If the noise is given in terms of the noise voltage density N, then the RMS voltage is calculated as
E = ( ∑ Nn2 ∙ Δfn) ½ ( VRMS )
Cool Feature You can implement this last equation in many SPICE simulators. Recalling that ONOISE represents the voltage spectral density N, simply add the following equation to the plot window. In PSPICE, this looks like
SQRT(SUM(ONOISE*ONOISE))
The far right of the graph shows the total RMS voltage of your circuit. (NOTE: You might have noticed that the frequency Δfn is absent from the equation above. Actually, the SUM function automatically calculates the Δfn term.)
CIRCUIT INSIGHT Simulate the SPICE file RES_NOISE.CIR with an EAMP gain =1, R1 = R2 = 100k, RLP1 = 100 and CLP1 = 1.59 nF. This time add the trace ONOISE to a plot window. Now, open a new plot window and add the trace SQRT(SUM(ONOISE*ONOISE)). What is the total RMS noise voltage at the highest frequency point of the graph?
HANDS-ON DESIGN You can experiment with values of R1, R2 and the low-pass filter to see the effect on RMS noise. Try increasing CLP1 do decrease the bandwidth. How does the bandwidth effect the total RMS noise? Did it go down with a smaller bandwidth as expected?
FINAL NOTE
Noise can be one of the more challenging and tougher design topics! Sometimes it takes a few trips around the block before it begins to make sense. Here are some helpful guides.
SPICE, A Guide to Circuit Simulation and Analysis Using PSPICE, P. Tuinenga, Prentice-Hall.
Low-Noise Electronic System Design, C. Motchenbacher and J. Connelly, John-Wiley and Sons, 1993.
Analysis and Design of Integrated Circuits, P. Gray and R. Meyer, John-Wiley and Sons, 1993.
SPICE FILE
Download the file or copy this netlist into a text file with the *.cir extension.
RES_NOISE.CIR - NOISE ANALYSIS: RESISTOR DIVIDER, AMP, AND LP FILTER * * RESISTOR DIVIDER V1 1 0 AC 1 DC 5 R1 1 2 100K R2 2 0 100K * * AMP AND LP FILTER EAMP 3 0 2 0 1 RLP1 3 4 100 CLP1 4 0 1.59NF * .AC DEC 5 100 100MEG .NOISE V(4) V1 5 .PRINT NOISE ONOISE .PROBE .END
© 2009 eCircuit Center