Switched-Capacitor Resistor
CIRCUIT
SWCAP_RES.CIR Download the SPICE file
So what's the big headache about fabricating an RC filter on a MOS integrated circuit? For starters, the biggest capacitor you'll get will be around 100 pF! Next, that means to create a low-pass filter with fc = 100 Hz, you'll need a resistor of R = 16 MΩ! Now, you've just lost a big chunk of real estate for one resistor! To make things worse, the resistor is highly non-linear and the tolerances are horrible. So what's the solution?
If you can't have a real resistor, why not a simulated one? All you need is a couple of switches and a capacitor - both readily available in MOS. And to boot, the capacitor ratios can be tightly controlled. Today switched-capacitor circuits are thriving in the field as mult-pole filter circuits and programmable analog ICs.
SIMULATED RESISTOR
First, let's define what our resistor needs to do. Given a potential difference in volts, get a proportional current to flow in Amps. Of course Amps is how many Coulombs per second (Q / s) will move through the resistor.
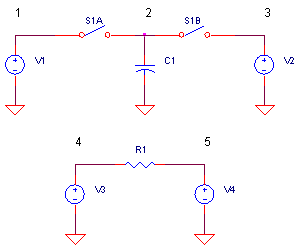
In the switched-capacitor circuit, S1A and S1B are alternately closed. As a result C1 is charged alternately to V1 and V2. Now, in order to change C1's voltage from V1 to V2, a charge (Coulombs) must flow from C1.
Δq = ΔV ∙ C = (V2 - V1) ∙ C
The same charge flows through S1A and S1B in sharp pulses each time one of the switches is closed. If these switches are opened / closed at a regular time interval Δt, you get an average current flowing. You can define this average current by the charged moved Δq divided by the time interval Δt.
![]()
Comparing this equation to ohms law
![]()
we see a simulated resistance!
![]()
The bottom line? Switching the capacitor moves a charge proportional to the voltage difference. The resistor achieves the same function only in a continuous manner. Using a water analogy, we can imagine a couple of scenarios: 1) a steady water flow, or 2) the same water delivered rapidly in buckets. Both create the same flow of water - on average!
SWITCHED-CAPACITOR CIRCUIT
Let's run a switched capacitor resistor, then compare it to a standard resistor. Switches S1A and S1B are turned ON and OFF by non-overlapping pulse generators VSA and VSB. The "resistor" is strung across voltage sources: V1 = 5V and V2 = 1V.
Suppose you need to simulate a 20 kΩ resistor. Given C1 = 1000 pF capacitor, how fast do you need to run the switches?
Δt = R ∙ C
= 20 kΩ ∙ 1000pF
= 20 μs
Given our "resistor", we expect a current to flow of (5 - 1) / 20 kΩ = 200 uA.
CIRCUIT INSIGHT
Run a SPICE simulation of SWCAP_RES.CIR. Plot the A clock
phase for S1A by adding trace V(10). To see the current through S1A, add a
plot window and add trace
I(S1A). Notice a current pulse every time V(10) goes HI (S1A ON). This
represents the charge moved to change C1's voltage from V2 to V1. Likewise,
plot the B phase clock V(11) and I(S1B). Aha! - a similar current pulse as
C1 changes from V1 to V2.
Now the question remains - given the current spikes, how much current is delivered on average? To do this, simply remove traces I(S1A) and I(S1B) and then plot AVG( I(S1B)) . (Many of SPICE's waveform viewers, like PSPICE, provide a number of math functions you can apply to the traces such as AVG( ).) The average current looks to be around around 200 μA.
Now, let's compare this to the continuous current through a standard 20 kΩ resistor across the similar voltages V3 and V4. Plotting I(R2) we shouldn't be too surprised to see a current of 200 μA. It appears the creation of a simulated resistor was a success!
HANDS-ON DESIGN Need a different value resistor? Just change C or Δt. As an example, you can create a resistor that's half the original by doubling C or halving Δt. To cut Δt in half, change the A and B phase clocks to look like:
VSA 10 0 PULSE(0V 5V 0US 0.1US 0.1US 2.5US 10US)
VSB 11 0 PULSE(0V 5V 5US 0.1US 0.1US 2.5US 10US)
Don't forget to change R1 to 10 kΩ for comparison. Did the current go up for both the standard and simulated resistor?
LOW-PASS FILTER
Okay, sharp current pulses aren't very useful in real circuits. But many applications are RC filter types where other capacitors smooth or average these current pulses into useful voltages. Let's try a simple RC low-pass filter. ( Reality Check: Most RC switched-capacitor filters in practice are op amp based. But this simple RC example illustrates how simulated resistors can approximate standard resistors in a filter circuit.)
First, replace V2 and V4 with 10 nF capacitors C2 and C4.
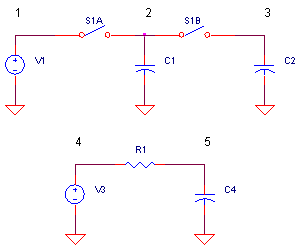
There are SPICE statements already in the file - simply comment out "*" the voltage sources and remove the comment symbol "*" from the capacitors. You'll also need to extend your simulation time to 1000 μs or so.
CIRCUIT INSIGHT Run a simulation of your filter circuits. Next, clear your plot windows and view the output voltages at V(3) and V(5). Okay now we are getting somewhere! The response of the simulated and standard filters look similar. But why does the switched-capacitor filter's output voltage appear as a stair-stepped waveform? This is the result of sharp current pulses being delivered to the C2. The capacitor simply does its job of accepting the total charge delivered and changing its voltage according (inversely-proportional) to its own capacitance value.
Try increasing or decreasing C2 and C4. When the C2 is made smaller than 10 nF, does the circuit do a better or worse job of approximating the standard RC circuit?
SWITCHED-CAPACITOR CIRCUITS
As mentioned before, many switched-capacitor circuits available today are op amp based. We'll take a look at some basic building blocks - like the the op amp integrator and the simple pole-zero filter - in future topics. In addition, the switched-capacitor resistor above has its problems - it can be very sensitive to stray capacitance. We'll also look at an improved switch arrangement that's more immune to the capacitive strays on an IC.
REFERENCES
Switched-Capacitor Circuit Design, R. Gregorian, et al, Proceedings of the IEEE, Vol 71, No. 8, August 1983.
SPICE FILE
Download the file or copy this netlist into a text file with the *.cir extension.
SWCAP_RES.CIR - SWITCHED-CAPACITOR RESISTOR * V1 1 0 DC 5V * * SWITCHES AND CAP S1A 1 2 10 0 SW1 C1 2 0 1000PF IC=0V S1B 2 3 11 0 SW1 * V2 3 0 DC 1V *C2 3 0 10NF * * SWITCH CONTROL VSA 10 0 PULSE(0V 5V 0US 0.1US 0.1US 5US 20US) VSB 11 0 PULSE(0V 5V 10US 0.1US 0.1US 5US 20US) * .MODEL SW1 VSWITCH(VOFF=0 VON=5 RON=100 ROFF=10MEG) * * * STANDARD RESISTOR V3 4 0 DC 5V R1 4 5 20K V4 5 0 DC 1V *C4 5 0 10NF IC=0V * * * ANALYSIS .TRAN 0.1US 100US * * VIEW RESULTS .PROBE .END
© 2004 eCircuit Center