Op Amp Diff Amp

eCircuit Center

Op Amp Summing Amplifier

CIRCUIT

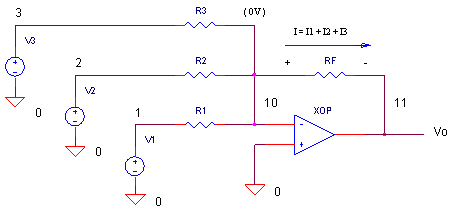OPSUM.CIR Download the SPICE file

The summing amplifier is a handy circuit enabling you to add several signals together. What are some examples? If you're measuring temperature, you can add a negative offset to make the display read "0" at the freezing point. On a precision amplifier, you may need to add a small voltage to cancel the offset error of the op amp itself. An audio mixer is another good example of adding waveforms (sounds) from different channels (vocals, instruments) together before sending the combined signal to a recorder.

Although, there are many ways to make a summer, this one is nice because it keeps the interaction between inputs at a minimum. What does that mean for you the designer? You can change the gain or add another input without messing with the gains of the other inputs. Just remember that the circuit also inverts the input signals. Not a big deal. If you need the opposite polarity, put an inverting stage before or after the summer.

SUMMING ACTION

How can you understand the summing action of this circuit keeping in mind the main "mission" of the op amp? Its mission is simple: keep the potential of the negative terminal very close to the positive terminal. In this case, keep the negative terminal close to 0V (virtual ground). The op amp essentially nails one leg of R1, R2 and R3 to a 0V potential. This makes it easy to write the currents in these resistors.

I1 = V1/R1; I2 = V2/R2; I3 = V3/R3

So what's the current I flowing in RF? According to our friend Kirchoff, we get

I = I1 + I2 + I3

Finally, notice that one leg of RF is also kept at 0V. So the output becomes Vo = -RF x I. Combining these pieces of information, we have a simple description of the amplifier

Vo = -RF·(V1/R1 + V2/R2 + V3/R3)

= -(V1·RF/R1 + V2·RF/R2
+ V3·RF/R3)

As you can see, the gain for each input can be controlled by a single resistor: K1 = -RF/R1,
K2 = -RF/R2 and K3 = -RF/R2.

LEVEL SHIFTER

Summing amplifiers make convenient level shifters. How could you transform an audio signal V1= +/-1.0V that's shifted into the input range of an ADC which is 0 to +2V?

You also have a -reference voltage available V2=-5V. You can pass the audio signal through R1 with gain K1=-1. You can also add in a +1.0V DC offset through R2 using the V2.

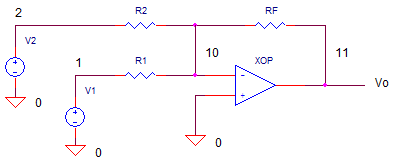
The gains and resistors are calculated as

Signal Gain
K1 = (+2V-0V)/(-1V- +1V)) = -1
R1 = -RF / K1 = 10k

Offset Gain
K2 = +1 / -5V = -0.2
R2 = -RF / K2 = 50k

CIRCUIT ANALYSIS Set R1=10k. (Initially, remove R2, R3 and V_2 and V_3 from the circuit by placing * in front the of their statements.) Only R1 and V1 should be in the circuit.

Then, run a TRAN simulation of OPSUM.CIR. Plot the output V(11) to see the output due to V1 only. The sine wave should swing positive and negative. Now, add R2 and V2 to the circuit by removing the * and rerun the simulation. Has the sine been shifted all positive as expected?

HANDS-ON DESIGN Change V1's amplitude by a factor of 2x. How do you need to change R1 and R2 to achieve the 0 to 2V input?

SIGNAL MIXER

In this circuit, there's three waveform - sine, square, and triangle- you can add any way you like. (Initially, remove R2, R3 and V2, V_2 and V_3 from the circuit by placing * in front the of their statements.). Initially, only R1 and V1 are in the circuit. But, you can add the other resistors by removing the * at the beginning of the R statement.

CIRCUIT ANALYSIS Run a simulation of OPSUM.CIR. Plot the output V(11) to see the output due to V1 only. What is the gain of V1 input? Because R1=RF=10k, the gain is - 10k / 10k = -1V/V. Now, add R2 and V_2 to the circuit by removing the * and rerun the simulation. Can you see the single cycle of the square wave added to the output V(11)? Add in R3 and V_3 to sum the triangle wave with the others. To look at the input sources themselves, add traces V(1) sine wave, V(2) square wave and V(3) triangle wave.

HANDS-ON DESIGN Suppose you need to add different amounts of each input. For example, to increase the square wave level by a factor of 10, decrease R2 to 1k making the gain GAIN_V2 = - RF/R2 = -10k/1k = -10. Check out your new output. Likewise, increase or decrease R1-R3 to see their effect on the output waveform.

CREATE WAVEFORMS WITH THE FOURIER SERIES

With the summing amplifier, you can add a number of sine waves together to generate various waveforms.

SPICE FILE

Download the file or copy this netlist into a text file with the *.cir extention.

OPSUM.CIR - OPAMP SUMMING AMPLIFIER
*
* SINEWAVE 4KHZ
V1	1	0	SIN(0V 1VPEAK 4KHZ)
* DC OFFSET
V2	2	0	DC	-5V
* SQUARE WAVE 100HZ
*V_2	2	0	PWL(0MS 1V   5MS 1V   5.01MS -1V   10MS -1V)   
* TRIANGLE WAVE 500HZ
*V_3	3	0	PWL(0MS -1V  1MS 1V  2MS -1V  3MS 1V  4MS -1V 
				+ 5MS 1V 6MS -1V 7MS 1V 8MS -1V 9MS 1V 10MS -1V)   
*
* INPUT Rs
R1	1	10	10K
*R2	2	10	10K
*R3	3	10	10K
* FEEDBACK R
RF	11	10	10K
*
* OPAMP
XOP	0 10	11	OPAMP1	
*
*
* OPAMP MACRO MODEL, SINGLE-POLE 
* connections:      non-inverting input
*                   |   inverting input
*                   |   |   output
*                   |   |   |
.SUBCKT OPAMP1      1   2   6
* INPUT IMPEDANCE
RIN	1	2	10MEG
* GAIN BW PRODUCT = 10MHZ
* DC GAIN (100K) AND POLE 1 (100HZ)
EGAIN	3 0	1 2	100K
RP1	3	4	1K
CP1	4	0	1.5915UF
* OUTPUT BUFFER AND RESISTANCE
EBUFFER	5 0	4 0	1
ROUT	5	6	10
.ENDS
*
* ANALYSIS 
.TRAN 	0.05MS  10MS
* VIEW RESULTS
.PROBE
.END

top