Wien Bridge Oscillator
CIRCUIT
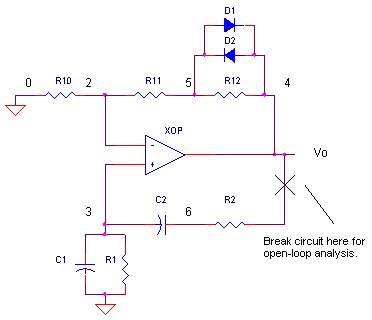
OPWIEN.CIR (Closed-Loop Circuit) Download the SPICE file
The opamp Wien-bridge oscillator provides a nice view into classic oscillator design using feedback analysis. Feedback analysis reveals if your circuit is stable (well behaved) or unstable (may oscillate). When designing amplifiers (especially high-speed ones), the trick is to avoid the conditions that make the circuit oscillate. When designing oscillators, you strive to achieve those conditions in a predictable way.
FEEDBACK ANALYSIS
Feedback analysis simply means opening the circuit and injecting an AC signal VTEST at one end of the circuit. Then, by looking at the magnitude (gain) and phase (time-shift) of signal as it travels around the opened loop, you can tell whether youíve got an amplifier or an oscillator on your hands.
When wearing your oscillator design hat, the idea is to pick components that will make the open-loop analysis meet the conditions for oscillation at your chosen frequency: The conditions are as follows:
If the AC gain around the opened loop is 1 V/V and the total phase shift is -360 or 0 deg, the circuit will oscillate at that frequency.
OPENING THE LOOP
Open the loop of the Wien Bridge Oscillator at the op ampís output. This is a good point because of the relatively low impedance of the output terminal. Likewise, VTEST also has a low output impedance. Therefore, opening the loop here does not significantly alter the circuitís behavior.
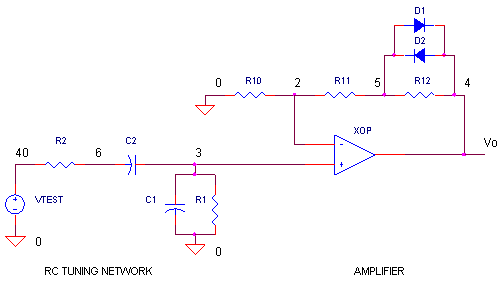
OPWIEN_OL.CIR (Open-Loop Circuit) Download the SPICE file
RC TUNING NETWORK
Two basic sections form the Wien-bridge oscillator: an RC tuning network and an amplifier. Both are necessary to achieve the conditions for oscillations. The RC network is characterized by a center frequency
![]()
where R=R1=R2 and C=C1=C2. At the center frequency, two interesting things occur at V(3). First, the phase shift goes through 0 degrees. And second, the magnitude reaches a peak of 1/3 V/V.
CIRCUIT ANALYSIS Run a SPICE simulation of the open-loop circuit OPWEIN_OL.CIR. Add trace VM(3) to see what the Magnitude looks like at the center frequency. For R1=R2=10k and C1=C2=16nF, the center frequency should be near 1 kHz. What does the phase look like? Add another plot window and then add trace VP(3) to see the Phase shift. The RC network does a nice job of meeting one of the conditions for oscillation: the phase is 0 degrees at the design frequency.
NON-INVERTING AMPLIFIER
The RC network falls short of the oscillation conditions in that the gain is only 1/3 V/V. How is the gain of 1V/V around the loop to be achieved? As you might have guessed, the non-inverting amplifier provides the needed gain. How much? A gain of 3 V/V makes the total gain 1/3 x 3 = 1 V/V. Setting the correct op amp gain is critical. Not enough - oscillations will cease. Too much Ė oscillation amplitude will grow until the output saturates.
Whatís needed is a mechanism to guarantee oscillations will start (GAIN > 3), yet, limit the gain (GAIN=3) at steady state. Enter our heros - D1, D2 and R12. The circuit adjusts its gain depending on the signal level. For small signals, the diodes do not conduct and the gain is set by
![]()
For larger signals, the voltage across R12 is big enough to make D1 and D2 conduct. The shunt resistance of the conducting diodes effectively reduces the R12 resistance, consequently, reducing the overall gain to GAIN=3.
CIRCUIT ANALYSIS Run a simulation of OPWIEN_OL.CIR. View the AC output of the op amp VM(4). For R10=10k, R11=18k and R12=5k, the op amp gain is (1 + (18+5)/10) = 3.3 V/V. This should make the overall open-loop gain equal to 1/3 x 3.3 = 1.1 V/V. Does the peak at VM(4) reach this expected gain?
OSCILLATOR OPERATION
Itís time to close the loop and try out the Wien-Bridge Oscillator. Run a simulation of closed-loop circuit OPWIEN.CIR and plot the Transient Analysis at V(4). How much time does it take for the amplitude to stabilize?
HANDS-ON DESIGN Design the circuit with a different oscillation frequency. Calculate the values for R and C. (Example: For fo = 10kHz, choose R1=R2=10k and calculate C1=C2=1/(2π x R1 x fo) = 1.6nF.) Test drive your oscillator. If thereís too little or too many sinewaves on the plot, adjust the total time of the Transient Analysis to another value like 5 ms by modifying the .TRAN statement to look like
.TRAN 0.05MS 5MS
If thereís no input signal to an oscillator, what starts the oscillations? Current source IS injects a pulse into the RC network to jump start the oscillations. In a real circuit, the large transient at power up will kick the circuit into action.
CIRCUIT INSIGHT What happens if thereís not enough gain around the loop? Reduce R12 to 1k making the total loop gain less than 1. Run a simulation. The circuit rings briefly, but thereís not enough gain to sustain oscillations.
SPICE FILES
Download the file or copy this netlist into a text file with the *.cir extention.
OPWIEN_OL.CIR - OPAMP WIEN-BRIDGE OSC, OPEN-LOOP ANALYSIS * VTEST 40 0 AC 1 * * RC TUNING R2 40 6 10K C2 6 3 16NF R1 3 0 10K C1 3 0 16NF * NON-INVERTING OPAMP R10 0 2 10K R11 2 5 18K XOP 3 2 4 OPAMP1 * AMPLITUDE STABILIZATION R12 5 4 5K *D1 5 4 D1N914 *D2 4 5 D1N914 * .model D1N914 D(Is=0.1p Rs=16 CJO=2p Tt=12n Bv=100 Ibv=0.1p) * * OPAMP MACRO MODEL, SINGLE-POLE * connections: non-inverting input * | inverting input * | | output * | | | .SUBCKT OPAMP1 1 2 6 * INPUT IMPEDANCE RIN 1 2 10MEG * DC GAIN (100K) AND POLE 1 (100HZ) EGAIN 3 0 1 2 100K RP1 3 4 1K CP1 4 0 1.5915UF * OUTPUT BUFFER AND RESISTANCE EBUFFER 5 0 4 0 1 ROUT 5 6 10 .ENDS * * * ANALYSIS .AC DEC 10 10 10MEG * VIEW RESULTS .PRINT AC VM(3) VP(3) .PLOT AC VM(3) VP(3) .PROBE .END
Download the file or copy this netlist into a text file with the *.cir extention.
OPWIEN.CIR - OPAMP WIEN-BRIDGE OSCILLATOR * * CURRENT PULSE TO START OSCILLATIONS IS 0 3 PWL(0US 0MA 10US 0.1MA 40US 0.1MA 50US 0MA 10MS 0MA) * * RC TUNING R2 4 6 10K C2 6 3 16NF R1 3 0 10K C1 3 0 16NF * NON-INVERTING OPAMP R10 0 2 10K R11 2 5 18K XOP 3 2 4 OPAMP1 * AMPLITUDE STABILIZATION R12 5 4 5K D1 5 4 D1N914 D2 4 5 D1N914 * .model D1N914 D(Is=0.1p Rs=16 CJO=2p Tt=12n Bv=100 Ibv=0.1p) * * SINGLE-POLE OPERATIONAL AMPLIFIER MACRO-MODEL * connections: non-inverting input * | inverting input * | | output * | | | .SUBCKT OPAMP1 1 2 6 * INPUT IMPEDANCE RIN 1 2 10MEG * DC GAIN (100K) AND POLE 1 (100HZ) EGAIN 3 0 1 2 100K RP1 3 4 1K CP1 4 0 1.5915UF * OUTPUT BUFFER AND RESISTANCE EBUFFER 5 0 4 0 1 ROUT 5 6 10 .ENDS * * ANALYSIS .TRAN 0.05MS 10MS * * VIEW RESULTS .PRINT TRAN V(4) .PLOT TRAN V(4) .PROBE .END
© 2002 eCircuit Center