Tune a PID Controller
CIRCUIT
PID1.CIR
SPICE netlist or
LTSPICE schematic
Right-click, select "Save link as..."
Tuning the PID controller can be like learning to roller blade, ski or maybe riding a bull. Until you've done it a few times, the literature you've read really doesn't hit home. But after after few attempts (and falls), you find it wasn't so bad after all - in fact it was kind of fun!
The PID controller is every where - temperature, motion, flow controllers - and its available in analog and digital forms. Why use it? It helps get your output (velocity, temperature, position) where you want it, in a short time, with minimal overshoot, and with little error. In many applications the PID controller can do the job - but as usual, with compromises. After a short intro to the PID terms and an example control system, you'll get a chance tune a PID controller.
THE PID CONTROLLER
You've probably seen the terms defined before: P -Proportional, I - Integral, D - Derivative. These terms describe three basic mathematical functions applied to the error signal , Verror = Vset - Vsensor. This error represents the difference between where you want to go (Vset), and where you're actually at (Vsensor). The controller performs the PID mathematical functions on the error and applies the their sum to a process (motor, heater, etc.) So simple, yet so powerful! If tuned correctly, the signal Vsensor should move closer to Vset.
Tuning a system means adjusting three multipliers Kp, Ki and Kd to add various amounts of each function to get the behavior you want. The table below summarizes the PID terms and their effect on a control system.
| Term | Math Function | Effect on Control System | |
| P Proportional |
KP x Verror | Typically the main drive in a control loop, KP reduces a large part of the overall error. | |
| I Integral |
KI x ∫ Verror dt | Reduces the final error in a system. Summing even a small error over time produces a drive signal large enough to move the system toward a smaller error. | |
| D Derivative |
KD x dVerror / dt | Counteracts the KP and KI terms when the output changes quickly. This helps reduce overshoot and ringing. It has no effect on final error. |
THE CONTROL SYSTEM
The SPICE circuit for the Control System looks pretty much like the block diagram.
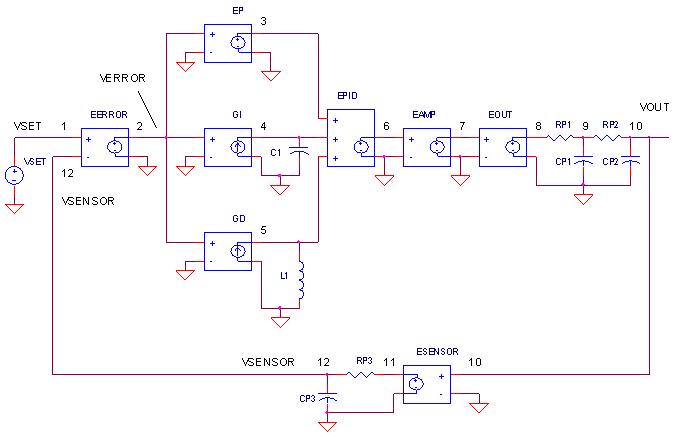
PID CONTROLLER. How do we create the PID terms?
Proportional term - EP multiples Verror at V(2) by a fixed gain of 1 - easy enough!
Integral term - GI converts V(2) to a current and integrates it on C1=1F.
Derivative term - GD converts V(2) to a current and forces it through L1. The voltage across L1 becomes V(5) = L1 di/dt. A quick substitution of L1=1H and i=Verror
gets you V(5) = dVerror/dt.OUTPUT PROCESS. EOUT represents a very simplified model of a process to be controlled like motor velocity or heater temperature. The gain of 100 could represent an output transfer function of 100 RPM / V or 100 ° C / V. To include the effects of the motor's inertia or heater's thermal mass, we've added some time delay into the output using two cascaded RC filters. Although Vout is simulated in volts, we know it really represents other variables like velocity in RPM or temperature in °C.
SENSOR. The sensor tells you, typically by a voltage, what's happening at the control system output. For motor velocity, a tachometer could generate 1 V / 100 RPM; for temperature, a thermistor circuit could produce 0.01 V / deg C. ESENSOR models this feedback device. Because a sensor does not respond instantly, an RC filter is also added here to model its finite response time.
TUNING THE PID CONTROLLER
Although you'll find many methods and theories on tuning a PID, here's a straight forward approach to get you up and soloing quickly.
1. SET KP. Starting with KP=1, KI=0 and KD=0, increase KP until the output starts overshooting and ringing significantly.
2. SET KD. Increase KD until the overshoot is reduced to an acceptable level.
3. SET KI. Increase KI until the final error is equal to zero.
HANDS-ON DESIGN Run a simulation of the circuit file PID1.CIR. VSET generates a 10V step input voltage to the control system. You can adjust the PID terms at the EPID source that adds the P, I and D terms at V(3), V(4) and V(5). Initially, the PID multipliers are set to KP=1, KI=0 and KD=0.
EPID 6 0 POLY(3) (3,0) (4,0) (5,0) 0 1 0 0
SET KP. Plot the system input V(1) and the sensor output (12). Although the response looks smooth, what is the sensor voltage compared to the desired 10V? The output falls short by 5V!
To reduce this error, increase KP to 10 (Change EPID multipliers to 10 0 0 ). Wow, the output now reaches 9V, reducing the error to 1V. But as you can see, the output is getting wild with overshoot and ringing. Push KP up higher to 20 or 30. Yes, the error reduces, but the overshoot gets worse. Eventually, your system will become unstable and break out into song (oscillate). Back off KP to 20 or so.
SET KD. The derivative term can rescue the response by counteracting the KP drive when the output is changing. Start with a small value like KD=0.2 and rerun the simulation (Change EPID multipliers to 20 0 0.2 ). Now you're wrestling control back into the system - the ringing and overshoot are reduced! Crank up KD some more. Improvement should continue to a point where the system becomes less stable and overshoot increases again. Return KD to around 0.5.
SET KI. With KP=20, KI=0 and KD=0.5 the response looks respectable, but the final error is a disappointing 0.5V (or 5%)! Now, try the KI term. This will integrate the remaining error into a drive signal big enough to reduce the error further. Start with KI = 10 ( EPID should look like 20 10 0.5 ). Check out the last half of the V(12) - the sensor output moves slowly toward 10V!
You might want to put up a cursor on the plot to monitor the exact value of V(12). The bigger you make KI, the faster it will move toward 10V. Like the other terms, a value is reached where the KI does more harm than good as the system becomes less stable.
DIVING DEEPER
Diving a little deeper you can get a clearer view of the PID components. Before we go beneath the surface, set KP=10, KI=0 and KD=0.
INSIDE P Run a couple of simulations with KP=10 and KP 20. Plot V(1) and V(12). What is the final error for each case? You may have noticed the errors of 1 and 0.5V are proportional to the gains of 10 and 20. You can estimate the error by
Verror ≈ Vset / KP
for large KP. What kind of gain do you need for a 1% error? You can easily calculate it as a gain of 100. However, we've already seen how large gain cause overshoot, ringing and oscillations! KP can't do it alone.
INSIDE D KD counteracts KP - let's see how. Set KP back to 10 and run a simulation. Plot the P function V(3) which is really Verror. Now plot the D term V(5) which we know is dVerror / dt. To get a good view of D, set the Y-Axis limits to +100 /-200V. Notice how dVerror / dt swings negative when Verror is initially positive. How does this help? Essentially D counteracts the P term potentially reducing ringing and oscillations.
The nice thing about the D term is that it goes to zero as the output settles. This makes sense - no change in output, no derivative term. Add in some of the D function by setting the multipliers to KP=10, KI=0 and KD=0.5. The initial overshoot should be significantly reduced.
INSIDE I We've seen how a large gain produces a small error. However, big KP gets you into big trouble with overshoot and ringing. Alternatively, an integrator can also give you a big gain by accumulating even a small error over time.
Run a simulation with KP=10, KI=0 and KD=0.5 and plot the I term at V(4). What does it look like? Notice, a ramp function, representing Verror integrated over over time, builds up to a significant drive voltage. Add in the I function by setting KP=10, KI=40 and KD=0.5. The I term completes the controller's job by moving the output toward an error of zero.
SIMULATION NOTE
Need a handy way to combine multiple signals such as the PID sum? A controlled source can be a function of multiple inputs in the form
V(6,0) = 0 + 10 ∙ V(3,0) + 2 ∙ V(4,0) + 1 ∙ V(5,0)
can be created by a VALUE defined by an expression.
EPID 6 0 VALUE = { V(3)*1 + V(4)*0 + V(5)*0 }
Or, created by a POLY function defined by a coefficient list at the end of the statement.
EPID 6 0 POLY(3) (3,0) (4,0) (5,0) 0 10 2 1
or more generally,
VO = k0 + k1∙V1 + k2∙V2 + k3∙V3
In fact, you can get higher order terms and cross terms by extending the coefficient list
VO = ...+ k4∙V1∙V1 + k5∙V1∙V2 + k6∙V1∙V3 +
+ k7∙V2∙V2 + k8∙V2∙V3 +
+ k9∙V3∙V3
If you're not using a term, you need to put a 0 in its place; you can't just leave it out. This feature is great for simpler polynomials. However, keeping track of the coefficient list for higher order polynomials can get crazy fast.
SPICE FILE
Download the file or copy this netlist into a text file with the *.cir extention.
PID1.CIR - THE PID CONTROLLER
*
* SET POINT
VSET 1 0 PWL(0MS 0MV 1MS 10V 2000MS 10V)
RSET 1 0 1MEG
*
* CALCULATE ERROR
EERROR 2 0 1 12 1
RERROR 2 0 1MEG
*
* P - PROPORTIONAL TERM
EP 3 0 2 0 1
RP 3 0 1MEG
*
* I - INTEGRAL TERM
GI 0 4 2 0 1
C1 4 0 1
R1 4 0 1MEG
*
* D - DERIVATIVE TERM
GD 0 5 2 0 1
L1 5 0 1
*
* ADD PID TERMS, ADJUST PID MULTIPLIERS
EPID 6 0 POLY(3) (3,0) (4,0) (5,0) 0 1 0 0
*EPID 6 0 VALUE = { V(3)*1 + V(4)*0 + V(5)*0 }
RPID 6 0 1MEG
*
* AMPLIFIER
EAMP 7 0 6 0 1
RAMP 7 0 1MEG
*
* PROCESS BLOCK WITH TIME LAG (PHASE SHIFT)
EOUT 8 0 7 0 100
RP1 8 9 100K
CP1 9 0 1UF
RP2 9 10 100K
CP2 10 0 1UF
*
* SENSOR BLOCK WITH TIME LAG
ESENSOR 11 0 10 0 0.01
RP3 11 12 10K
CP3 12 0 1UF
*
* ANALYSIS
.TRAN 10MS 2000MS
*
* VIEW RESULTS
*.PRINT TRAN V(1) V(12)
.PROBE
.END
LTSPICE FILE
An LTSPICE Schematic
has been added recently!
Right click the link and select "Save
link as..."
Adjust the PID parameters using .param Kp=1 Ki=0 Kd=0.
Run the simulation and add traces V(1) and V(12).
© 2002 - 2025 eCircuit Center