Sallen-Key Low-Pass Filter
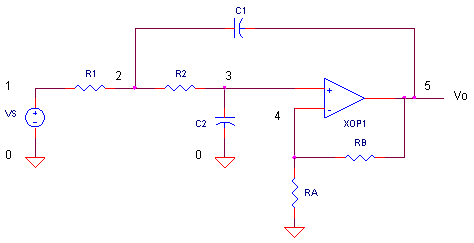
CIRCUIT
OPSALKEY1.CIR Download the SPICE file
Suppose you had a large interfering signal you needed to get rid of. To get lots of attenuation, you could cascade several RC filters. Unfortunately, the impedance of one RC section affects the next. This means that the “knee” or transition between the pass and stop bands won’t be very sharp. A sharp knee helps you reduce the interfering signal without degrading your desired signals. In this situation, the Sallen-Key active filter can save the day. This circuit implements a 2-pole filter. Cascading several stages can give you a steep attenuation curve with a very sharp knee.
LOW-PASS FILTER DESIGN
Although there are many filter types and ways to implement them, here’s an active low-pass filter that’s greatly simplified if R1=R2 and the op amp stage is a unity gain follower (RB=short and RA=open). Designing a 2-pole Butterworth filter requires just a few steps.
1. Choose a cutoff frequency fo (Hz).
As an example, select fo=10 kHz to reduce a noise signal at 50 kHz and pass your desired signals below 5 kHz.
2. Pick a convenient cap value C2 between 100pF and 0.1 uF.
Suppose you’ve got plenty of 1000pF caps in stock, select this value for C2.
3. Make C1 = 2 x C2
C1 = 2 · C2 = 2000pF
4. Calculate R1 = R2 = 0.707 / (2 · π · fo · C2)
R1 = R2 = 0.707 / (2 · π · 10kHz · 1000pF) = 11.2 K ohms
CIRCUIT ANALYSIS Take the Sallen-Key for a test drive and watch the frequency response at the output V(5). To get a better view of the attenuation past 10kHz, change the Y axis to a log scale. How fast does the curve decrease as the frequency increases by a factor of 10?
Just how much of an advantage does a 2-pole filter have over a single pole filter? There’s a simple RC filter (R10,C10) in the SPICE file for comparison. Both filters have a cutoff frequency of 10kHz. Add the output of the simple RC filter V(10) to your plot. Is there a difference in the attenuation of the stop bands? Another advantage of the active filter is that the knee hasn’t lost its sharpness.
HANDS-ON DESIGN Pick a different cutoff frequency for a low pass filter. Design your new filter and take a look at the output V(5).
FILTER LIMITS
In theory, the response in the stop band should keep decreasing as frequency increases. Instead, the response actually will begin rising again at some high frequency. Why? A properly functioning op amp is essential to the filter’s operation. However, real world op amps lose voltage gain at some frequency due to their finite bandwidth.
CIRCUIT INSIGHT Extend the frequency range of the analysis to 100 MHz via the command
.AC 10 100 100MEG
At what frequency does the curve depart from the ideal? This should be near the Gain Bandwidth Product GBP of the op amp.
HIGH-PASS FILTERS
HANDS-ON DESIGN Its easy to convert a Sallen-Key low-pass filter to a high-pass filter. Just swap the resistor and capacitor locations – R1 with C1 and R2 with C2. Here are the components with the exchanged node numbers.
R1 3 0 11.2K
R2 2 5 11.2K
C2 2 3 1NF
C1 1 2 2NF
Try out the high-pass circuit and plot the output V(5). Essentially, this response should be a mirror image of the low-pass flipped about the cutoff frequency. Again, due to the finite bandwidth of the op amp, the response is the pass-band (ideally flat) takes a nose dive beyond the GBP.
SINGLE POLE FILTER
If you need less attenuation in the stop band, try a single-pole RC low-pass filter with op amp buffer.
SIMULATION NOTE
To create a unity gain amplifier with XOP1, the circuit requires RB = (short circuit) and RA = (open circuit). To do this, the resistors were given small and large like RB=10 ohms and RA = 100MEG. Another way to open or remove a component is to place a "*" in the beginning of the statement. SPICE ignores these statements.
Be careful of using resistor values covering large ranges in the same circuit such as 1 Pico (1e-12) ohm and 1 Tera (1e+12) ohm. The computation required may be beyond the mathematical precision of the computer. To be safe, a range spanning 12 decades (say 1ohm to 1 Giga ohm) should be safe for double precision math.
SPICE FILE
Download the file or copy this netlist into a text file with the *.cir extention.
OPSALKEY1.CIR - OPAMP SALLEN-KEY LOW-PASS FILTER * 2ND-ORDER BUTTERWORTH * VS 1 0 AC 1 * R1 1 2 11.2K R2 2 3 11.2K C1 2 5 2000PF C2 3 0 1000PF * * UNITY GAIN AMPLIFIER, RA=OPEN, RB=SHORT RA 4 0 100MEG RB 4 5 1 XOP 3 4 5 OPAMP1 * * SINGLE RC FILTER FOR COMPARISON R10 1 10 15.9K C10 10 0 1000PF * * OPAMP MACRO MODEL, SINGLE-POLE * connections: non-inverting input * | inverting input * | | output * | | | .SUBCKT OPAMP1 1 2 6 * INPUT IMPEDANCE RIN 1 2 10MEG * DC GAIN (100K) AND POLE 1 (100HZ) * GBWP = 10MHz EGAIN 3 0 1 2 100K RP1 3 4 1K CP1 4 0 1.5915UF * OUTPUT BUFFER AND RESISTANCE EBUFFER 5 0 4 0 1 ROUT 5 6 10 .ENDS * * ANALYSIS .AC DEC 10 100 1MEG * VIEW RESULTS .PLOT AC V(5) .PROBE .END
© 2002 eCircuit Center