Thermistor Preamp
CIRCUIT
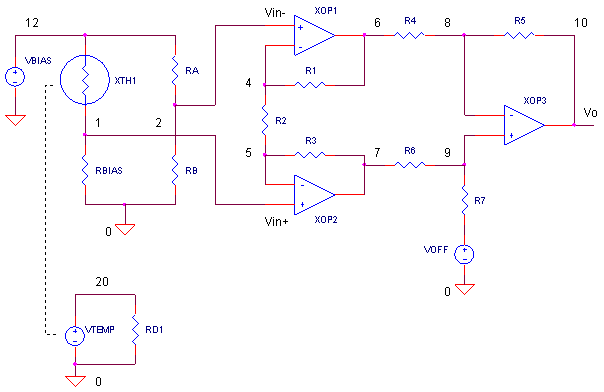
THERM_PREAMP.CIR Download the SPICE file
Suppose you're asked to design a circuit using a thermistor that measures room temperature,
0 °C (32 °F) to 40 °C (102 °F). The circuit's output
should be scaled to 0.1 V / °C such that a Digital Voltmeter (DVM) can
directly display the temperature. Choosing an appropriate bias resistor, you
can transform the thermistor's highly non-linear R vs. T curve into a linear
voltage. But, how do you choose the gain and offset of your preamp? How
accurate is the reading between calibration points? How hot or cold of
a temperature can you measure before the sensor's non-linearity sends the
error beyond
+/- 1 °C? Armed with a SPICE circuit, an Excel Spreadsheet and a
couple rules-of-thumb you can design a decent circuit complete with life's
compromises and trade-offs.
SENSOR BRIDGE
SENSOR Part of your design challenge is using a thermistor that's already stocked by the company. The specs look like Ro = 10 kΩ at To = 25 °C, Beta = 3450. The highly non-linear Rth vs. T curve is predicted by
![]()
where the temperatures in the equation are in K.
BIAS RESISTOR An easy way to straighten out the Rth vs. T curve is by adding a series bias resistor. What value? A good rule of thumb - choose a bias resistor to have the same value that the thermistor exhibits in the middle of your measurement range. For starters we'll choose RBIAS = 10 kΩ, the thermistor's nominal value at 25 °C.
You may have noticed the thermistor placed in the top leg of the bridge. Given the thermistor's negative temperature coefficient, this creates a positive voltage change as T increases.
![]()
BIAS VOLTAGE SUBTRACTION Components VBIAS = 5V, RBIAS = 10 kΩ and Rth = 10 kΩ at 25 °C create a bias voltage of 2.5 V at the sensor. How can you subtract it before passing the sensor's output to the next stage? That's where the other leg of the sensor bridge comes in. Resistors RA = RB = 10 kΩ together with VBIAS = 5 V produce a handy Vref = 2.5 V that gets subtracted from the thermistor's voltage by the instrumentation amp. The bridge's output voltage is described as
VS = Vsens - Vref
INSTRUMENTATION AMP
GAIN Here's the classic 3
op amp instrumentation amp. It amplifies the input
voltage difference
(VS = Vin+ - Vin-) according to
![]()
where R1=R3 and R4 = R5 = R6 = R7. All of the gain is housed in the first stage, XOP1 and XOP2.
OFFSET To plumb in an offset, just drive R7 with a voltage, VOFF. The same offset appears at the output! The complete equation describing the output looks like this
![]()
which can be simply rewritten as the familiar equation of a line.
y = m x + b
The trick now lies in choosing m and b to produce Vo = 0.1 V / °C.
CHOOSING GAIN AND OFFSET
The equation y = m x + b transforms the sensor's output x into the desired output y. For example, if we let x0 be a point in the sensors output, then y0 is the desired output of the amplifier.
y0 = m ∙ x0 + b
Picking another sensor voltage x1, the output becomes
y1 = m ∙ x1 + b
From these two equations and two unknowns, we can easily find m and b!
![]()
b = y0 - m ∙ x0
THE REAL DEAL
Let's pull it all together with a real example. Using an Excel spreadsheet Thermistor_Preamp.xls, you can see the big picture of the sensor chain. Over a large temperature range, the spreadsheet calculates the sensor resistance Rth, the sensor voltage Vsens, and the differential output of the bridge Vsens - Vref. Check out the curve of the highly non-linear Rth vs. T graph. At first glance, it appears almost useless! But a simple resistor RBIAS converts it to a reasonably linear voltage as shown in the Vsens - Vref graph.
First, choose a couple of calibration points like the end-points of our range, T = 0 and 40 °C. Here are the numbers for the two temperatures.
| Temp | Rth | Vsens |
VS = Vsens - Vref (x) |
Desired Vout
0.1 V/°C (y) |
|
| 0 °C | 28.84 kΩ | 1.29 V | -1.21 V | 0.0 V | |
| 40 °C | 5.74 kΩ | 3.18 V | + 0.68 V | 4.0 V |
Next, calculate the slope and offset for your preamp.
| m = (y1 - y0) / (x1 - x0) = (4.0 - 0.0) / (0.68 - -1.21) = 2.1184 |
b = y0 - m∙x0 = 0.0 - 2.1184∙-1.21 = 2.569 |
So what kind of Vo vs. T output does the preamp produce? The spreadsheet calculates the preamp output y = m∙x+ b. For comparison, the spreadsheet graphs this actual preamp output, along with the desired output, a linear line between 0 (0 °C) and 4 V (40 °C). How close are they? At what temperatures do they go their separate ways?
To make the preamp a reality, you need to calculate the gain resistor R2 of the instrumentation amplifier. For R1 = R3 = 10 kΩ, R2 becomes
R2 = 2∙R1 / (m - 1)
= 2∙10k / (2.1184 - 1)
= 17.883 kΩ
Given the tolerances of the sensor and other resistors, you might want to make R1 some combination of a resistor and a potentiometer for a precise gain adjustment.
Finally, set VOFF = b = 2.569 V. In real life, VOFF can be derived from a resistor divider hung from VBIAS followed by a unity-gain op amp buffer. Exchange one of the resistors for a potentiometer and you've got yourself an offset adjustment.
SPICE TIME
Voltage source VTEMP generates a ramp from 0 to 40V representing temperature from 0 to 40 °C. Thermistor XTH1 is defined by subcircuit NTC_10k, a Negative Temperature Coefficient (NTC) device with a resistance value of 10 kΩ at 25 °C.
CIRCUIT INSIGHT Run a simulation of THERM_PREAMP.CIR. Take a look at the bridge output by plotting V(1) - V(2). Next, view the preamp's output by plotting V(10). As you can see, the preamp does a nice job of transforming the bridge's output into a very readable 0 to 4 V achieving the 0.1 V / C design goal.
Although the preamp's output looks fairly linear, how straight is it? Let's check the error between the calibration points by plotting 10*V(10) - V(20) where 10*V(10) converts the preamp's output directly to °C. V(20) is the output of VTEMP. Not too bad! The error is near 0 at the calibration points as expected! But in between, the sensor shows its non-linear nature. The maximum error should be around 0.8 C.
HANDS-ON DESIGN Is there a better value for RBIAS that reduces the maximum error? Try a different RBIAS value. Use the spreadsheet to help calculate your new gain and offset.
Rerun the simulation over a larger temperature range like -10 C to 50 °C. (In the VTEMP statement, change the voltage points to 0 and 50.) How quickly does the error grow at temperatures outside the calibration points of 0 and 40 °C.
HANDS-ON DESIGN Try your hand at designing a sensor preamp over a different temperature range. Suppose your range must be optimized for reading body temperature 95 to 10°5 F. Choose RBIAS to be some value in the middle of the range, then calculate your slope and offset. Use the spreadsheet if you wish. How accurate is your new sensor circuit?
PRECISION PARTS, ADJUSTMENTS AND TRADEOFFS
Of course, the wonderful results we achieved above assumed perfect components - the thermistor Resistance / Beta, op amps, resistors, bias voltage were all spot on! Reality, being not so kind, says all of these parts come with tolerances. Depending on the accuracy required and budget available, you have several options. Pay a premium for precision parts that you can drop into the circuit to meet your spec. Or, include offset / gain adjustments and invest your money in calibration time on the manufacturing floor.
REFRESHER NOTES
This circuit pulls together many topics - thermistor model, linearized thermistor, sensor bridge, instrumentation amp, subcircuits, and op amp models. You can browse other circuits and topics at the Circuit Collection.
SPICE FILE
Download the file or copy this netlist into a text file with the *.cir extension.
THERM_PREAMP.CIR - THERMISTOR WITH PREAMP GAIN AND OFFSET
*
* TEMPERATURE
VTEMP 20 0 PWL(0MS 0DEG 100MS 40DEG)
RD1 10 0 1MEG
*
* SENSOR BRIDGE
VBIAS 12 0 DC 5V
XTH1 12 1 20 0 NTC_10K
RBIAS 1 0 10K
RA 12 2 10K
RB 2 0 10K
*
* 3 OPAMP INSTRUMENTATION AMPLIFIER
* GAIN STAGE
XOP1 2 4 6 OPAMP1
R1 4 6 10K
R2 4 5 17.883K
R3 5 7 10K
XOP2 1 5 7 OPAMP1
* DIFF AMP
R4 6 8 10K
R5 8 10 10K
R6 7 9 10K
R7 9 11 10K
XOP3 9 8 10 OPAMP1
VOFF 11 0 DC 2.569V
*
* MEASUREMENT ERROR
E_ERR 21 0 VALUE = { V(10)*10-V(20)}
R_ERR 21 0 1MEG
*
* THERMISTOR SUBCIRCUIT ****************************************
* thermistor terminals : 1,2
* temperature (deg C) input+,-: 4,5
*
.SUBCKT NTC_10K 1 2 4 5
ETHERM 1 3 VALUE={i(VSENSE)*10K*EXP(3450/(V(4,5)+273.15)-3450/(25+273.15))}
VSENSE 3 2 DC 0
.ENDS
*
* OPAMP MACRO MODEL, SINGLE-POLE *******************************
* connections: non-inverting input
* | inverting input
* | | output
* | | |
.SUBCKT OPAMP1 1 2 6
* INPUT IMPEDANCE
RIN 1 2 10MEG
* GAIN BANDWIDTH PRODUCT = 10MHZ
* DC GAIN (100K) AND POLE 1 (100HZ)
EGAIN 3 0 1 2 100K
RP1 3 4 1K
CP1 4 0 1.5915UF
* OUTPUT BUFFER AND RESISTANCE
EBUFFER 5 0 4 0 1
ROUT 5 6 10
.ENDS
*
*
* ANALYSIS
.TRAN 1MS 100MS
*
* VIEW RESULTS
.PRINT TRAN V(1) V(10)
.PROBE
.END
© 2004 eCircuit Center